Introduction
Overall System and Reference Frames
Attached is a detailed drawing of the system, illustrating all the frames in use, complete with frame labels. These frames and their labels have been consistently used and identified in the code to maintain clarity and coherence.
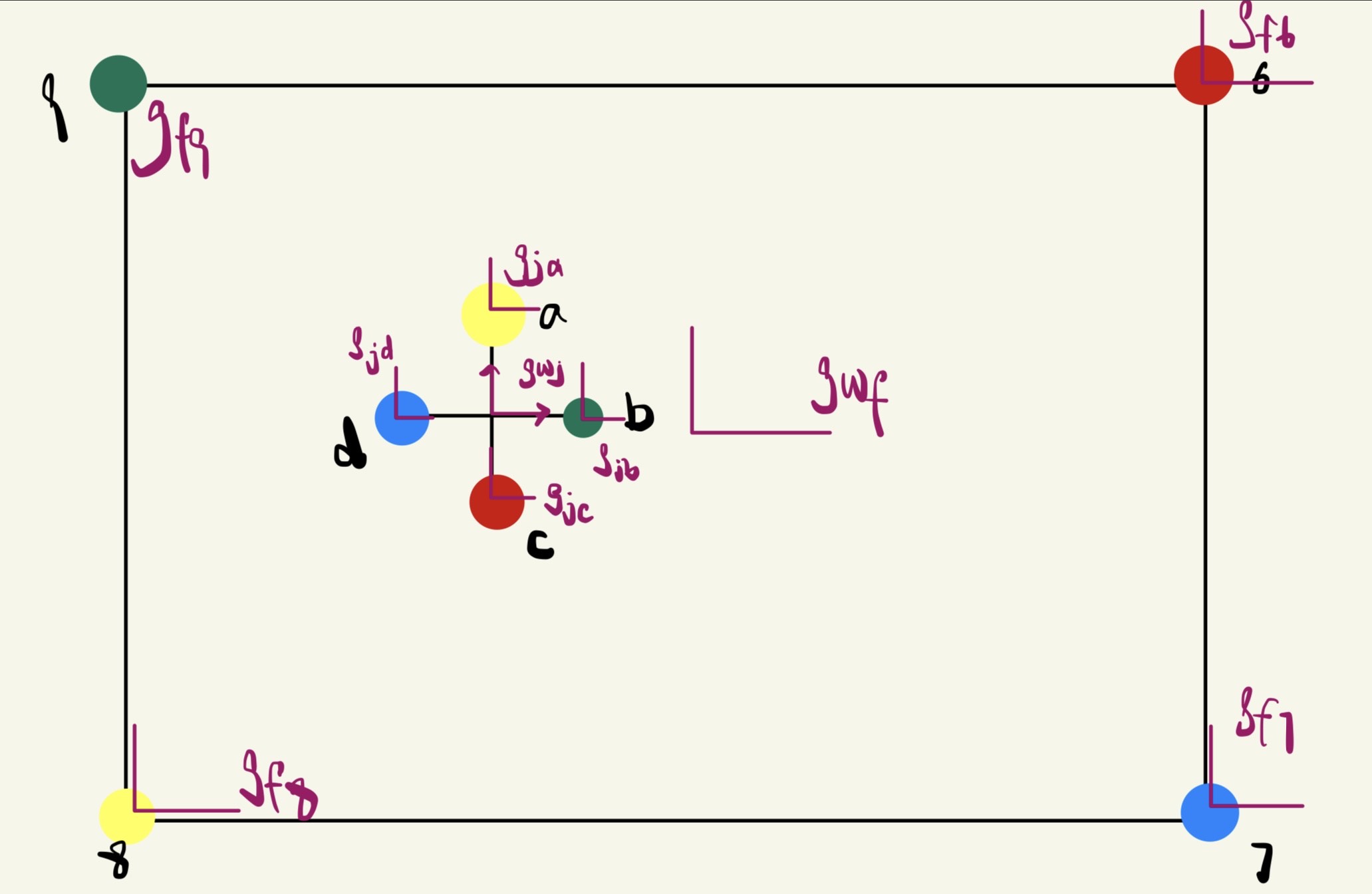
Frames
The base frame for the box is called g_wf, where f is the center of the box. g_f6, g_f7, g_f8, g_f9 are the relative frames based on the box center. The frame between world and box vertices can be generated through cross product of g_wf and g_f6, g_f7, g_f8, g_f9.
The base frame for the jack is called g_wj, where j is the center of the jack. g_jb, g_ja, g_jc, g_jd are the relative frames based on the box center. The frame between world and box vertices can be generated through cross product of g_wj and g_jb, g_ja, g_jc, g_jd.
Euler-Lagrange Equations
The Euler Lagrange equation is calculated based on the:
Considering uniform mass distribution in both box and jack, I calculate the kinetic and potential energy at the centroid (geometric center of the two rectangles). And Lagrangian as kinetic minus the potential energy of the two bodies.L = KE - V, where KE is kinetic energy of both jack and box and V is the potential energy of both jack and box. Using the Euler lagrange formula to get the equations of motion, by equating it to the external force applied on both the rigid bodies.
The python script calculating the kinetic energy KE and potential energy V is shown below:
#Kinetic Energy and Potential Energy
#frame kinetic energy
KE_frame = sym.simplify(0.5*(v_wf).T*Inertia_frame_mat*v_wf)
#jack kinetic energy
KE_vwa = sym.simplify(0.5*(v_wa).T*Inertia_jack_mat*v_wa)
KE_vwb = sym.simplify(0.5*(v_wb).T*Inertia_jack_mat*v_wb)
KE_vwc = sym.simplify(0.5*(v_wc).T*Inertia_jack_mat*v_wc)
KE_vwd = sym.simplify(0.5*(v_wd).T*Inertia_jack_mat*v_wd)
KE_jack = sym.simplify(KE_vwa + KE_vwb + KE_vwc + KE_vwd)
KE_total = sym.simplify(KE_jack+ KE_frame)
hf = sym.simplify(sym.Matrix([g_wf[1,3]]))
h_wa = sym.simplify(sym.Matrix([g_wa[1,3]]))
h_wb = sym.simplify(sym.Matrix([g_wb[1,3]]))
h_wc = sym.simplify(sym.Matrix([g_wc[1,3]]))
h_wd = sym.simplify(sym.Matrix([g_wd[1,3]]))
V_f = Mf*gravity*hf[0]
V_wa = m_j_point*gravity*h_wa[0]
V_wb = m_j_point*gravity*h_wb[0]
V_wc = m_j_point*gravity*h_wc[0]
V_wd = m_j_point*gravity*h_wd[0]
V_total = sym.simplify(sym.Matrix([V_f + V_wa + V_wb + V_wc + V_wd]))
System variables:
Define system variables as q = [x_f, y_f, theta_f, x_j, y_j, theta_j] and use Lagrangian Equation and q to calculate Euler-Lagrangian Equation.
External force:
The box is supposed to vibrate and have some degree of gravity compensation, so I have given the external force in y as 4M_boxg [ M_box*g : is the force due to gravity, and 4 is a tunable parameter, could be any hard-set value, but its easier to reference wrt to gravitational force, so used this.] And the external force on theta is a sinusoidal function, to generate an oscillation/ vibration like motion. And there is no external force to jack (it has potential component, but that is internal).
Impact conditions:
There are 16 impact conditions in this model. Which is that every 4 point of the jack coming in contact with any of the box’s walls. Which basically means that the x component of transform (between corner and wall) for Wall 1 and 3 and y coordinate for Wall 2 and 4, should be less than a threshold value. Value should not be kept 0, as in simulation, till the 0 transform is actually achieved the animation would have stepped outside the box, as it is a bit coarsely discrete system. Also, this threshold value can be tuned. And I used it to detect the impact occurrence and calling the impact update function.
Impact update procedure:
To find the state of the system after impact, we solve six conservation of momentum equations and one Hamiltonian conservation equation. We have 7 variables (lambda, and six state variables [q]) and 7 equations. And I used this to generate the trajectory after every impact.
Simulated trajectory plots:
Box-Motion:
Box-Velocity:
Jack-Motion:
Jack-Velocity:
Simulation Behavior Analysis:
When any of the four corners of the jack comes in contact with any of the four walls of the box [ i.e. impact condition is met], the jack bounces off the wall and keeping the speed of jack same, as I am assuming elastic collision [ i.e. following the impact update rule].
Also, the external force ensures the box does not free fall under gravity. If you uncomment the external force section, this behavior can be seen in the simulation as well. Also, as a sanity check, one may uncomment impact equations, and it would be observed that, both the bodies would have free fall decoupled from each other.